AtCoder Beginner Contest 194: E – Mex Minの初心者解説（トリッキーな最小値探索）

Software
2021.03.13

計算量を抑えて最小値の探索を行うのがコツで，今回の問題ではこの能力が問われました．E問題レベルになると説明がかなり難しく，自分の日本語力が問われているような気がします…

問題

公式の問題はコチラ．

問題文

$\mathrm{mex}(x_1, x_2, \ldots, x_k)$ を $x_1, x_2, \ldots, x_k$ に含まれない最小の非負整数と定義する．

ここで，長さ $N$ の整数列 $A = (A_1, A_2, \ldots, A_N)$ を考える．$0 \leq i \leq N-M$ を満たす全ての整数 $i$ について $\mathrm{mex}(A_{i+1}, A_{i+2}, \ldots, A_{i+M})$ を計算したとき，この最小値を求めなさい．

制約

  • $1 \leq M \leq N \leq 1.5 \times 10^6$
  • $0 \leq A_i < N$
  • 入力に含まれる値は全て整数

解説

公式の解説はコチラ．今回もヤマカサさんのブログが非常に参考になりました．

mexってなんだ？

まず，問題文の $\mathrm{mex}(x_1, x_2, \ldots, x_k)$ の理解が私には難しかったので例題を通して確認します．

たとえば，以下の例題を考えると，

  • 例1：$X_1 = (x_1, x_2, x_3) = (1, 2, 5)$
  • 例2：$X_2 = (x_1, x_2, x_3) = (0, 2, 5)$
  • 例3：$X_3 = (x_1, x_2, x_3) = (0, 2, 1)$

それぞれ，以下のようになります．

  • $\mathrm{mex} \, X_1 = 0$
  • $\mathrm{mex} \, X_2 = 1$
  • $\mathrm{mex} \, X_3 = 3$

$\mathrm{mex} \, X$ は集合 $X$ に含まれない最小の非負整数なので，例1のように 0 か，例2のように歯抜けになっている数字か，例3のように集合に含まれる数字よりも 1 大きい数字が答えになります．

制約について考える

制約その1：$1 \leq M \leq N \leq 1.5 \times 10^6$

AtCoder では $2 \times 10^8$ 程度までの計算が可能である（参考サイト）ことを考えると，$O(N)$ もしくは $O(N \log N)$ 程度の計算までしかできないことになります．$O(N^2)$ の計算は TLE してしまうということです．

制約その2：$0 \leq A_i < N$

この制約は問題を解く上で非常に重要かと思います．次節で集合 $A$ に含まれる整数の個数をカウントする配列 $B$ を用意するのですが，この制約により配列 $B$ の大きさを $N$ に制限できます．

考え方詳細

問題の解法を詳細に考えていきます．

集合 $A_{iM}$ を $A_{iM} = (A_{i+1}, A_{i+2}, \ldots, A_{i+M})$ とおきます．（$0 \leq i \leq N-M$）

ここで，$A_{iM}$ に含まれる整数の頻度を格納する大きさ $N$ の配列 $B$ を考えると，この配列 $B$ の値が 0 となる整数のうち最小のものが $A_{iM}$ の最小値（すなわち $\mathrm{mex} \, A_{iM}$）となります．

※このとき，制約その2があることによって，$B$ の配列の大きさは $N$ となります．

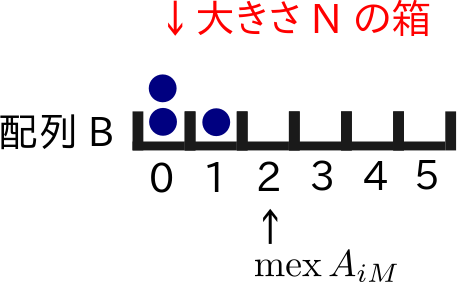
たとえば，$N = 6, i = 0, M =3, (A_1, A_2, \ldots, A_6) = (0, 0, 1, 5, 2, 2)$ の状況を考えると，配列 $A_{iM} = (0, 0, 1)$ となり，$\mathrm{mex} \, A_{iM} = 2$ となります．

  • $B[0] = 2$
  • $B[1] = 1$
  • $B[2] = 0$
  • $B[3] = 0$
  • $B[4] = 0$
  • $B[5] = 0$

図解するとこんな感じですね．

図は配列 $B$ の中に 2 個 0 が含まれ，1 個 1 が含まれることを表しています．

さらに，$i$ を $0 \leq i \leq N-M$ の範囲で動かしていき，最小値を取れば答えが導き出せます．

  • $i = 1$ のとき，$(B[0], B[1], \ldots, B[5]) = (1, 1, 0, 0, 0, 1)$ より $\mathrm{mex} \, A_{iM} = 2$
  • $i = 2$ のとき，$(B[0], B[1], \ldots, B[5]) = (0, 1, 1, 0, 0, 1)$ より $\mathrm{mex} \, A_{iM} = 0$
  • $i = 3$ のとき，$(B[0], B[1], \ldots, B[5]) = (0, 0, 2, 0, 0, 1)$ より $\mathrm{mex} \, A_{iM} = 0$

といった具合です．この例題の場合，答えは 0 です．

ソースコード

ステップ1：配列 $B$ を定義し，$i = 0$ のときの $\mathrm{mex} \, A_{iM}$ を求める．

ステップ2：$i$ を $1 \leq i \leq N-M$ の間で動かしたときの配列 $B$ から，$\mathrm{mex} \, A_{iM}$ の最小値を求める．

ステップ2の処理が少しむずかしいかもしれないので，ソースコードの意味を文章で説明します．実際の処理はソースコードを見てみてください．

$(A_{j}, A_{j+1}, \ldots, A_{j+M-1})$ に含まれる整数の頻度を表す $B_j$ と $(A_{j+1}, A_{j+2}, \ldots, A_{j+M})$ に含まれる整数の頻度を表す $B_{j+1}$ を考えると，$B_j$ と $B_{j+1}$ の関係は以下のようになります．

  • $B_{j+1}[A_{j}] = B_j[A_{j}] -1$
  • $B_{j+1}[A_{j+M}] = B_j[A_{j+M}] +1$

さらに，更新後の $B$ で $B[A_{j}]$ が 0 になっていたら，現在の答えと $A_{j}$ を比較して小さい方を答えとします．更新後に $B[A_{j}]$ が 0 になるのは，更新後の集合 $(A_{j+1}, A_{j+2}, \ldots, A_{j+M})$ に $A_{j}$ の数字が 1 つも含まれなくなったことを意味します．

この更新を $1 \leq i \leq N-M$ の範囲で繰り返して最終的な答えを得ます．

ソースコードは以下のような感じです．問題文の添字は $A_1$ から始まっていてソースコードは $A_0$ から始まっているため，わかりにくい部分もあるかもしれませんがご容赦ください…

#include <bits/stdc++.h>
#include <math.h>
#include <string>
using namespace std;

int main(void) {
    int N, M;
    cin >> N >> M;
    vector<int> A(N, 0);
    vector<int> B(N, 0);
    for (int i=0; i<N; i++) {
        cin >> A[i];
    }

    // step 1
    for (int i=0; i<M; i++) {
        B[A[i]]++;
    }
    int ans = N;
    for (int i=0; i<N; i++) {
        if (B[i] == 0) {
            ans = i;
            break;
        }
    }

    // step 2
    for (int i=0; i<N-M; i++) {
        B[A[i]]--;
        B[A[i+M]]++;
        if (B[A[i]] == 0) {
            ans = min(ans, A[i]);
        }
    }

    cout << ans << endl;

    return 0;
}

以下のサイトを参考に書いたので，かなりソースコードは似た感じに仕上がってしまいました．

[AtCoder] ABC 194 E – Mex Min | ヤマカサの競技プログラミング
問題 方針 セットとマップによる値の管理 まず初めに、セットに \( 1 \) から \( M \) までの値を入れます。次に、先頭から \( M \) 個までの \( M \)...
yamakasa.net

まとめ

ちょっとトリッキーな最小値探索でした．一つずつ領域をずらしながら最小値を探索していくという類ですね．勉強になりました．

コメント