しばらくブログ更新をサボっていたのですが、久しぶりに更新します。私事ですが、最近自動搬送ロボットを開発しているベンチャー企業に転職し制御周りのソフトウェアエンジニアになったので、制御関連の記事を書いていきたいなーと思っています。まずは、大学のときに専門だった非線形制御について書いていこうと思います。
ベースとして HASSAN K. KHALIL の NONLINEAR CONTROL という本を題材にします。今回は CHAPTER 2. TWO-DIMENTIONAL SYSTEMS をまとめます。
本を読んでみて気になった点・勉強になった点をまとめてみるというのがこの記事の趣旨です。
概要
以下のような微分方程式で表される2次元のシステムを考え、$(x_1, x_2)$ がどのように変化するかを考察します。
$$ \dot x_1 = f_1(x_1, x_2), \ \dot x_2 = f_2(x_1, x_2)$$
ベクトル場の軌跡
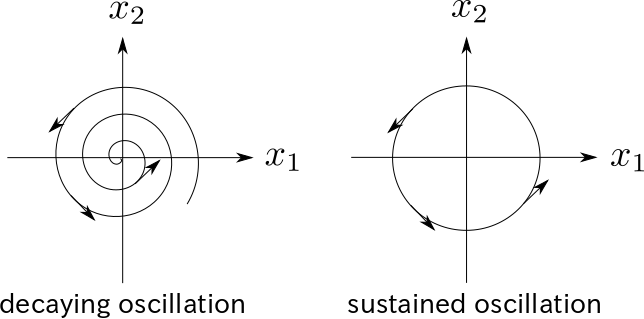
二次元平面上のそれぞれの点でベクトル場を書いてみると、状態がどのように遷移するかを確認することができます。たとえば、以下の図は左図が $(x_1, x_2)$ が原点に収束していく場合、右図が周期運動を永遠に繰り返す場合のベクトル場の軌跡を示しています。矢印はその点でのベクトル場を表しています。
あとで出てきますが、上左図は空気抵抗を考慮した場合の振子のベクトル場の軌跡、上右図は空気抵抗を考慮しない場合の振子のベクトル場の軌跡をイメージすると直感的にわかりやすいかと思います。空気抵抗を考えないと永遠に振り子は振動し続けますが、実際には空気抵抗のせいで振動は途中で止まりますよね。
非線形システムの平衡点付近での定性的なふるまい
二次元の線形システムの phase portrait(ベクトル場の軌跡)がどのようになるかは、NONLINEAR CONTROL の p.17〜p.21 に書いてあります。
$$\dot x = A x$$
の $A$ の固有値が (a) 実数か複素数か (b) 実部が負か正かゼロかで phase portrait が大きく異なります。簡単に説明すると、(i) 実部が負の場合は原点に収束、(ii) 正の場合は発散といった形です。ここらへんの説明は複雑なので本書を読んでもらった方がいい気がします。すいません…。
さて、非線形システムの平衡点付近でのふるまいは、線形近似システムの平衡点でのふるまいと基本的に同一になります。平衡点 $(p_1, p_2)$ は $f_1 (p_1, p_2) = f_2(p_1, p_2) = 0$ を満たす点のことです。
なので、非線形システムの平衡点近傍でのふるまいは、以下の線形近似システムの固有値から判定できるということになります。
$$
a_{11} = \left. \frac{\partial f_1(x_1, x_2)}{\partial x_1} \right|_{x_1 = p_1, \ x_2 = p_2}, \
a_{12} = \left. \frac{\partial f_1(x_1, x_2)}{\partial x_2} \right|_{x_1 = p_1, \ x_2 = p_2}
$$
$$
a_{21} = \left. \frac{\partial f_2(x_1, x_2)}{\partial x_1} \right|_{x_1 = p_1, \ x_2 = p_2}, \
a_{22} = \left. \frac{\partial f_2(x_1, x_2)}{\partial x_2} \right|_{x_1 = p_1, \ x_2 = p_2}
$$
$$
\dot y =
\begin{bmatrix}
a_{11} & a_{12} \\
a_{21} & a_{22}
\end{bmatrix}
y
= Ay
$$
この $A$ をヤコビアン行列をよびます。
ただ、線形近似したシステムの固有値の実部がゼロである場合には注意が必要で、非線形要素を考慮した解析をする必要があります。これはざっくり言うと、固有値の実部が負の場合と正の場合でシステムの挙動が大きく異なるため、固有値がそのちょうど中間にある場合のふるまいを近似したシステムで解析するのはちょっと乱暴だねという話みたいです。
振子のモデリング
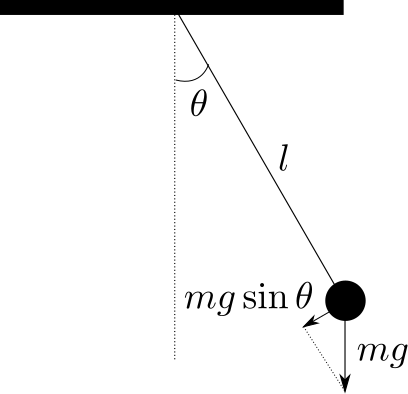
振子には上図のような力が加わります。数式にすると以下のようになります。
$$ml^2 \frac{d^2 \theta}{dt^2} \ = \ T \ – \ mgl \sin \theta \ – \ kl^2 \frac{d \theta}{dt} $$
ここで、$T$ は外力(トルク)、$\theta$ が振子の傾き、$m$ がおもりの質量、$g$ は重力加速度、$l$ は振り子の長さ、$k$ は空気抵抗係数を表しています。回転運動なので、トルクベースで考えるということに注意します。
振子のふるまい
振子は、振子の傾き $\theta$ とその時間微分 $\dot \theta$ を状態として考えることで、状態が $(\theta, \dot \theta)$ の二次元システムとして捉えることができます。
空気抵抗を考えない場合
外力と空気抵抗はないものと仮定し、さらに計算を簡単化するために $m, g, l, k$ の係数をすべて 1 である場合を考えます。
すると、以下の式が成り立ちます。
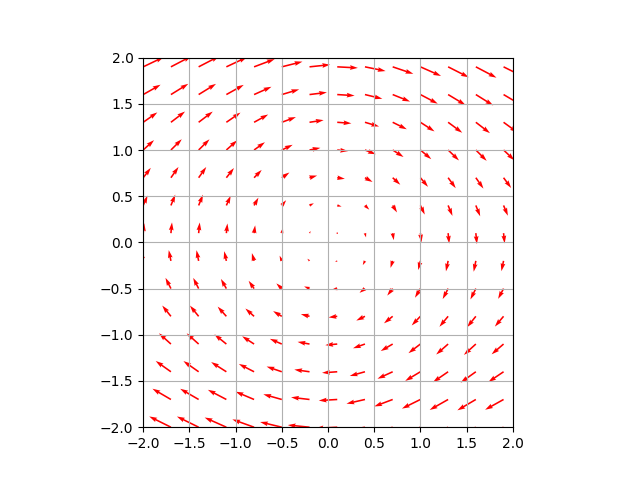
$$ \ddot \theta \ = \ – \sin \theta$$
これを python の quiver 関数を使って $(\theta, \dot \theta)$ をプロットしてみると、以下のようになります。
使用した python コードは以下のとおりです。
import numpy as np
import matplotlib.pyplot as plt
plt.figure()
# environmental settings
LX, LY=2.0,2.0 # parameter for mesh
gridwidth=0.3
X, Y= np.meshgrid(np.arange(-LX, LX, gridwidth), np.arange(-LY, LY, gridwidth)) # create mesh
# define vector funcitons
U = Y
V = -np.sin(X)
# draw graphs
plt.quiver(X,Y,U,V,color='red') # plot vector field
plt.axis([-LX, LX, -LY, LY], 'equal')
plt.gca().set_aspect("equal")
plt.grid()
plt.draw()
plt.show()空気抵抗を考える場合
空気抵抗がある場合に上と同様の仮定を適用すると、以下の式が成り立ちます。
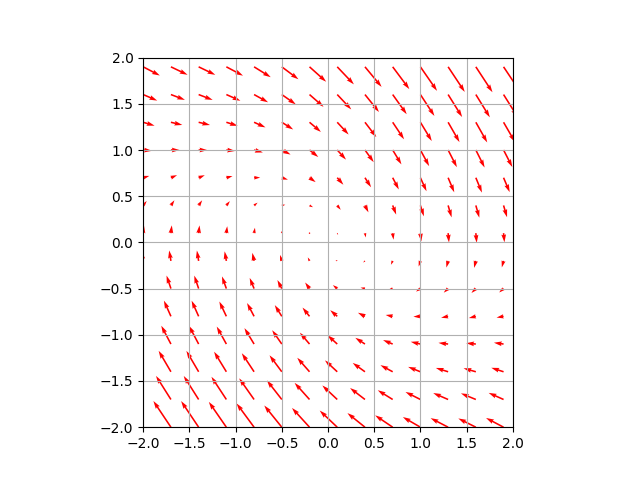
$$ \ddot \theta \ = \ – \sin \theta \ – \ \dot \theta$$
$(\theta, \dot \theta)$ をプロットした結果は以下のようになります。
ちょっとわかりにくいかもですが、ベクトル場が原点に収束する方向に向いているのがわかるかと思います。
これらから、空気抵抗を考慮しなかった場合は $(\theta, \dot \theta)$ が周期運動を繰り返し、考慮した場合は $(\theta, \dot \theta)$ が原点 $(0, 0)$ にいずれ収束することがわかります。
複数の平衡点
非線形システムは、複数の独立した平衡点を持っている場合があります。例えば、上の例の振子もその一例です。ちなみに、線形システムでは $(0, 0)$ に独立した平衡点を一つ持つか、連続した平衡点のセットを持つかのいずれかです。
振子の例では、空気抵抗を考慮しない場合・考慮する場合のいずれでも $(0, 0)$ と $(\pi, 0)$ に平衡点を持っています。ただ、$(\pi, 0)$ の平衡点近傍では少しでも外乱が入ると発散してしまうため、倒立振子の制御等を行わない限りこの状態にとどめておくことはできません。
これは、振子の線形近似システムが以下のようなり、
$$ \dot x =
\begin{bmatrix}
0 & 1 \\
-\cos x_1 & -1
\end{bmatrix}
x
$$
$x_1 = 0, \pi$ におけるヤコビアン行列と固有値が以下のようになることから説明がつきます。
$$
A_0 =
\begin{bmatrix}
0 & 1 \\
-1 & -1
\end{bmatrix}, \ \text{固有値} = \frac{-1 \pm \sqrt{3}i}{2}
$$
$$
A_\pi =
\begin{bmatrix}
0 & 1 \\
1 & -1
\end{bmatrix}, \ \text{固有値} = \frac{-1 \pm \sqrt{5}}{2}
$$
$(\theta_1, \theta_2) = (0, 0)$ の場合のヤコビアン行列の固有値が両方とも負で安定な平衡点になっているのに対し、$(\theta_1, \theta_2) = (\pi, 0)$ の場合の固有値は正と負で平衡点がサドルになっています。
リミットサイクル
独立した閉軌道のことで、安定したリミットサイクルでは無限時間経つとその軌道上に収束するようです。Van der Pol oscillatorが有名だそうです。
まとめ・感想
二次元システムを考えると状態変数がどのように遷移できるを図で視覚的に確認できるので、理解しやすくなりますね。
もし何か誤り等あれば、遠慮なくコメントお願いいたします。

コメント